▍BSM模型诞生背景

自19世纪出现有组织的场外期权市场后，如何确定一个期权的价值，就逐渐引起了业界和学界的关注。对于一只流通的股票，我们可以很容易从市场上观测到它的价格，如果流动性足够好，我们观测到的价格也会接近真实的价值。然而对于衍生品，特别是场外衍生品，其价格将很难被观测到。模型的作用，就是提供一种估值方法，让人们能通过流动性较好的且已知价格的证券，推算出其他流动性较差的证券价值。

关于期权定价模型的研究由来已久。自19世纪20年代布朗运动被提出后，1900年法国的金融学家劳伦斯·巴施里耶（Louis Bachelier）就将布朗运动引入了他的期权定价模型中，随后越来越多的科学家以布朗运动为基础对资产价值进行建模。直到1973年，斯坦福大学教授迈伦·斯克尔斯（Myron Scholes）和他的同事、已故数学家费雪·布莱克（Fisher Black）合作研究出了一个较为完整的期权定价模型。与此同时，哈佛商学院教授罗伯特·默顿（Robert Merton）也发现了同样的公式及许多其它关于期权的有效结论。两篇论文几乎同时在不同刊物上发表。因此，Black-Scholes模型（BS模型）亦可称为Black-Scholes-Merton模型（BSM模型）。默顿拓展了原模型的内涵，丰富了BSM模型的可应用场景。

假设资产价格服从几何布朗运动的经典BSM模型在提出后被业界广为接受，从此到1987年的美国金融危机，市场上期权的价格与BSM模型几乎吻合，仅在不同期限上因为波动率的调整而有微量的偏离。即使1987年金融危机后，市场依旧以BSM模型下的隐含波动率来描述期权的价格。

▍BSM模型假设

（1）期权为期末行权的欧式期权；

（2）标的资产在期权存续期内无分红；

（3）能做多及做空任意数量的标的资产；

（4）标的资产价格服从几何布朗运动；

（5）市场无摩擦，即不存在税收和交易成本；

（6）短期无风险利率在期权存续期内恒定且可知；

（7）股价收益率服从正态分布，收益率的波动率恒定且可知。

现金和债券作为最基本的资产，他们的价格会影响几乎所有的衍生品价格。在违约率很低的前提下，银行储蓄账户利息、国债利率、LIBOR等都可以用作无风险资产收益的近似。基于连续复利的模型抽象，我们可以得到最基本的无风险资产价格模型。

不失一般性，货币市场账户的动态过程可以写为：

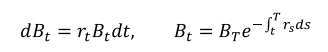
但在BSM模型中，假设（6）将无风险利率设定为常数，因此：

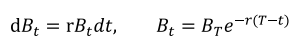
【免责声明】本文信息仅用于投资者教育之目的，不构成对投资者的任何投资建议，投资者不应当以该等信息取代其独立判断或仅根据该等信息作出决策。本文信息力求准确可靠，但对这些信息的准确性或完整性不作保证，亦不对因使用该等信息而引发或可能引发的损失承担任何责任。